Every Computer You've Ever Used Is Mathematically Suboptimal

The story of computing is filled with elegant solutions born from practical constraints. Binary computing—the foundation of every smartphone, laptop, and server humming around us—represents one of humanity's greatest engineering achievements. Yet from a purely mathematical perspective, there's a more efficient path we never took.

What makes this story even more fascinating? The optimal solution is governed by the same mathematical constant that describes population growth, compound interest, and radioactive decay.

Understanding Binary: The Foundation We Built

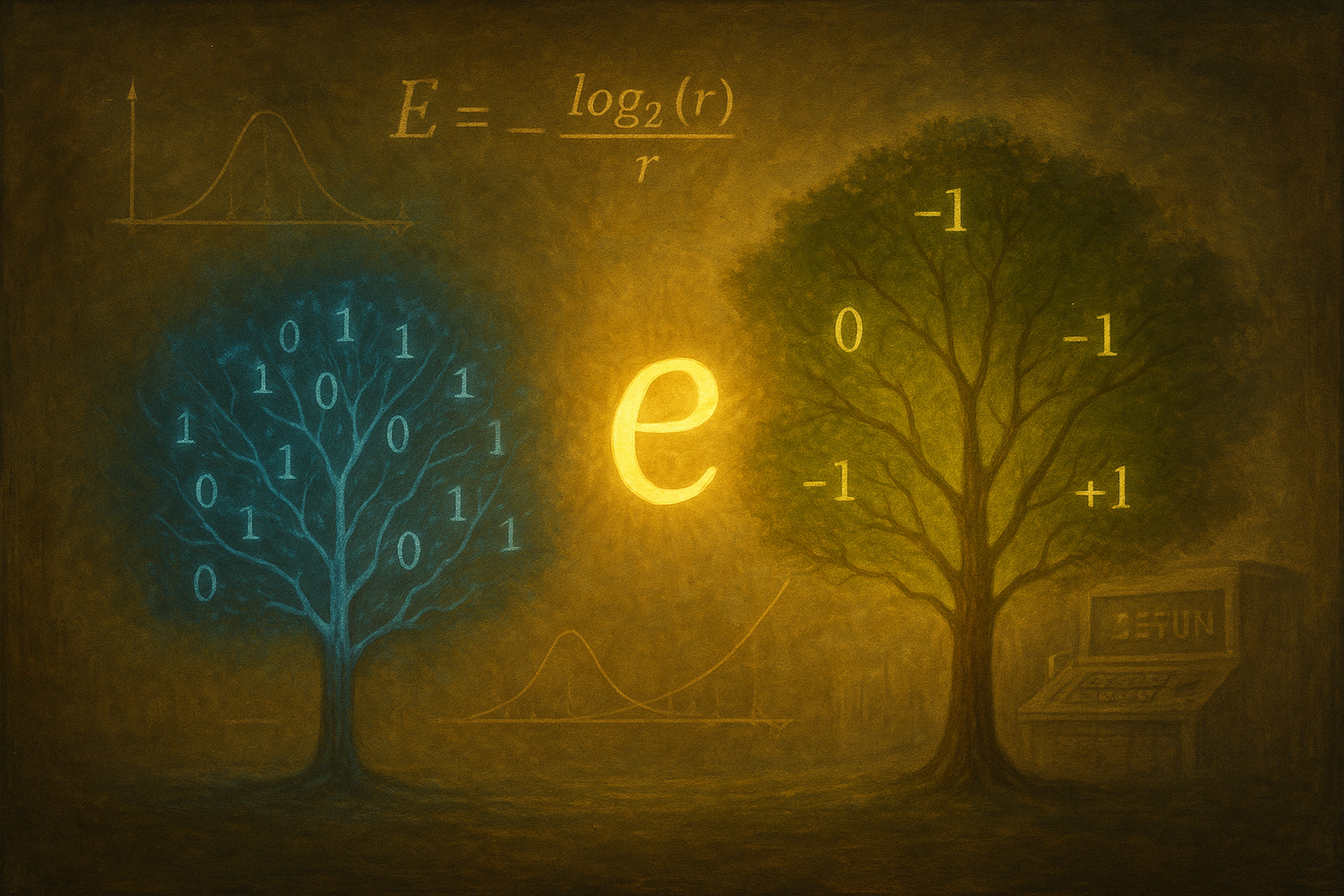
Binary systems operate on beautifully simple two-level logic: on or off, high or low voltage. Each position in a binary number can represent exactly two states, which we call 0 and 1. This simplicity became the bedrock of the digital revolution, enabling the creation of reliable, mass-producible computer systems.

The elegance of binary lies in its clarity. A switch is either on or off—there's no ambiguity, no middle ground to misinterpret. This binary certainty allowed engineers 80 years ago to build the first reliable digital computers with the technology available to them.

The Mathematics of Information: Why Ternary Carries More

To understand why ternary might be superior, we need to dive into information theory—one of the most beautiful branches of mathematics.

Here's the key insight: information is fundamentally about distinguishing between possibilities. The more possibilities you can distinguish, the more information you can encode.

In information theory, we measure information using a logarithmic scale. If you have r possible symbols to choose from, each symbol carries log₂(r) bits of information. Let's break this down:

Why logarithms? Because information compounds exponentially. With 2 binary digits, you get 2² = 4 combinations. With 3 binary digits, you get 2³ = 8 combinations. The logarithm inverts this relationship: if you can distinguish between 8 possibilities, you need log₂(8) = 3 bits to encode that information.

The mathematical derivation:

• Binary (2 symbols): log₂(2) = 1.000 bit per symbol
• Ternary (3 symbols): log₂(3) ≈ 1.585 bits per symbol
• Decimal (10 symbols): log₂(10) ≈ 3.322 bits per symbol

The key takeaway: A ternary digit carries exactly 58.5% more information per digit than binary—a precise mathematical relationship describing how information scales with choices.

But observant readers will notice something intriguing: decimal carries even more information per symbol at 3.322 bits. So why isn't base-10 the obvious winner? The answer reveals one of mathematics' most elegant optimization principles.

The Mathematical Sweet Spot: Euler's Number Reveals the Truth

While decimal digits carry even more information per symbol, there's a crucial trade-off between information density and implementation complexity. This is where mathematics reveals something profound about the fundamental nature of efficiency itself.

The efficiency of any number system is captured by this elegant equation:

Efficiency E(r) = log₂(r) / r

Where:

• Numerator (log₂(r)): Information content per symbol
• Denominator (r): Hardware complexity (number of voltage levels to maintain)

Here's where mathematics becomes breathtaking: when you solve for the maximum of this function using calculus, you get r = e ≈ 2.718...

Yes, that's Euler's number—the same mathematical constant that governs the most fundamental processes in nature:

• Compound interest: Jacob Bernoulli discovered e while studying continuous compound interest, finding that (1 + 1/n)^n approaches e as n approaches infinity
• Population growth: Exponential growth models using e^(rt) describe how bacteria, populations, and biological systems naturally expand
• Radioactive decay: The exponential decay function e^(-λt) describes how radioactive materials lose energy over time
• Normal distribution: The probability density function that describes countless natural phenomena contains e in its mathematical foundation
• Continuous processes: Any system where the rate of change is proportional to the current value naturally involves Euler's number

The profound implication: The optimal base for information systems is governed by the same fundamental constant that describes optimal growth and decay processes throughout the natural world. Mathematics is revealing that base-e ≈ 2.718 represents the perfect balance between information density and complexity—a universal principle of efficiency.

Since we can't build a 2.718-base computer, ternary (base-3) is the closest integer approximation to mathematical perfection.

A Practical Example: The Million-Number Challenge

Let's examine the cost of representing 999,999 (nearly one million) different numbers across different systems:

Decimal System: 999,999 (6 digits)

• Needs 6 positions, each distinguishing 10 voltage levels
• Total complexity: 10 × 6 = 60 "units of engineering difficulty"

Binary System: 11110100001000111111 (20 bits)

• Needs 20 positions, each distinguishing 2 voltage levels
• Total complexity: 2 × 20 = 40 units

Ternary System: 1212210202000 (13 trits)

• Needs 13 positions, each distinguishing 3 voltage levels
• Total complexity: 3 × 13 = 39 units

The mathematical beauty: Ternary achieves the lowest total complexity by finding the optimal balance—fewer positions than binary, simpler per-position requirements than decimal. This isn't coincidence; it's the mathematical inevitable result of being closest to base-e.

The Soviet Experiment: Setun and the Road Not Taken

The story becomes even more compelling when we realize that ternary computing wasn't just theoretical speculation—it was actually built and proven to work.

In 1958, at Moscow State University, Nikolay Brusentsov and his team under the leadership of Sergei Sobolev developed the world's first ternary computer: Setun. The computer was completed in December 1958 and worked correctly from the first run, without even requiring debugging.

Fifty Setun computers were manufactured between 1959 and 1965, and they were deployed across the Soviet Union—from Kaliningrad to Yakutsk, from Ashkhabad to Novosibirsk—serving universities, research laboratories, and plants. The experience confirmed significant advantages of ternary computing: the computers were simpler to manufacture, more reliable, and required less equipment and power than their binary counterparts.

But the timing was catastrophic. By 1958, IBM and Western computing companies had already fully committed to binary-based transistor computers, with massive investments and established supply chains. Although the Setun performed equally well as contemporary binary computers, and cost 2.5 times less to produce, the global computing ecosystem had already locked onto binary standards.

The Soviet government eventually decided to abandon original computer designs and encouraged cloning of existing Western systems to align with global standards. Brusentsov's lab was relocated to a windowless attic in a student dormitory, support was withdrawn, and the original Setun prototype—which had worked faithfully for seventeen years—was destroyed.

The lesson: Mathematical optimality means nothing if it arrives after the infrastructure has already committed to a suboptimal path. The Setun project perfectly demonstrates how technological momentum can override mathematical truth.

Balanced Ternary: Mathematical Elegance in Number Representation

There's an even more elegant variant of ternary computing called "balanced ternary," which reveals something beautiful about the nature of numbers themselves.

Using -1, 0, +1 Instead of 0, 1, 2 Is Mathematically More Elegant

In binary representation, negative numbers require additional complexity:

• The number 2 = 10 (2 bits)
• The number -2 = 10 + sign bit = 110 (3 bits)

But balanced ternary uses three symmetric states:

• -1 (negative)
• 0 (zero)
• +1 (positive)

Signs are built into the system! To make any number negative, you simply flip each digit's sign:

• Number 5 in balanced ternary: 1(-1)(-1)
• Number -5 in balanced ternary: (-1)(1)(1)

This symmetry isn't just elegant—it's computationally powerful. Many algorithms become simpler when the number system naturally handles positive and negative values with equal ease. Binary computers require complex schemes like two's complement arithmetic, while balanced ternary makes the symmetry of mathematics explicit in the hardware.

Why We're Still Stuck with Binary: The Infrastructure Lock-In

If ternary is mathematically superior, and the Soviets proved it could work, why does every computer still use binary? The answer reveals how technological systems become locked into suboptimal paths.

The engineering challenge of the 1940s: Voltage is inherently noisy and unstable. In the 1940s, reliably distinguishing between three voltage levels (low, medium, high) was exponentially more difficult than simply detecting "high" or "low." With vacuum tubes and early transistors, binary's two-state simplicity was the only feasible path to reliable computation.

The historical lock-in: Engineers in the 1940s unknowingly chose the less mathematically optimal system—not because they made the wrong decision, but because mathematics demanded engineering capabilities that wouldn't exist for decades. By the time those capabilities emerged in the late 1950s, the entire computing industry had already committed enormous resources to binary infrastructure.

The network effect: Once binary became standard, every component, every software system, every manufacturing process, and every engineer's education reinforced that choice. The cost of switching became prohibitive, even as the technology to support ternary became available.

This mirrors other examples in technology history where suboptimal solutions become permanently locked in: the QWERTY keyboard layout, the width of railroad tracks, the choice of AC vs. DC power systems.

The Universal Language of Information

Here's something fascinating: we measure all information in "bits" regardless of the storage system, just like we measure all energy in "joules" whether it comes from coal, solar, or nuclear power.

When we say a ternary digit carries "1.585 bits," we're using binary digits as the universal unit of information measurement. It's like saying "this ternary digit is worth 1.585 binary digits in information content."

Why "bits" became universal: Binary computing arrived first, and information theory developed alongside early binary computers. The term "bit" (binary digit) became the standard unit because it defined the field, much like how "horsepower" still measures car engines long after horses left the roads.

The Breakthrough: Patents Prove Seamless Transition is Possible

The story takes a dramatic turn when we realize that the final barrier to ternary computing has fallen. Recent patent developments have proven that we can build ternary chips using the exact same infrastructure we use for binary chips today.

The game-changing discovery: In September 2023, Huawei filed a groundbreaking patent (CN119652311A) demonstrating "stable operation of ternary logic gates through a fully digital CMOS architecture." The breakthrough uses existing threshold voltage layering technology to map input signals to 0V (0), 1.65V (+1), and 3.3V (-1), implementing ternary operations through standard transistor combination logic.

What makes this revolutionary: Multiple patents and research papers now demonstrate how existing CMOS manufacturing processes can fabricate ternary logic circuits using standard foundry layers—the same ACTIVE, POLY, METAL1 layers used in every chip factory today. Successful implementations have been demonstrated on both 130nm and 90nm foundry processes.

The infrastructure revelation: T-CMOS (Tunneling-CMOS) technology enables ternary logic implementation using conventional CMOS fabrication methods. The key insight is that existing semiconductor foundries can produce ternary chips without requiring new manufacturing equipment or processes—only modifications to voltage control and transistor design.

This means semiconductor manufacturers can transition to ternary production using their existing billion-dollar fabrication facilities. No new factories, no new equipment, no new supply chains. The mathematical optimum can finally be achieved using the infrastructure we already have.

The convergence moment: Just as mathematical optimization predicted, the engineering challenges that forced us toward binary 80 years ago have been solved precisely when we need maximum computational efficiency for AI, climate modeling, and scientific simulation. Experimental results show ternary implementations can reduce transistor count by 40% and dynamic power consumption to 1/3 of binary circuits.

The Path Forward: Evolution, Not Revolution

Binary computing deserves profound respect. It enabled the digital revolution, connected the world, and brought powerful computation to billions of people. The engineers who chose binary made exactly the right decision with the technology available to them.

But mathematics doesn't care about historical constraints. The optimal computer has always been ternary—we just needed eight decades of technological progress to build it.

The transition ahead: Moving from binary to ternary isn't about replacing a flawed system—it's about evolution. Just as we moved from vacuum tubes to transistors to integrated circuits, the shift to ternary represents our ongoing journey to align engineering reality with mathematical truth.

As we stand at the threshold of this transition, we're witnessing something remarkable: the moment when human engineering capability finally catches up to mathematical inevitability, guided by the same universal constant that governs growth, optimization, and efficiency throughout nature.

The most optimal computer has always been written in the language of mathematics. We're finally learning to speak it fluently.

---

In the end, the story of ternary computing isn't just about better processors—it's about the beautiful persistence of mathematical truth, waiting patiently through decades of technological development for the moment when reality could finally match theory.